
Regolatore PID– definizione, funzione, configurazione & utilizzo
I controllori PID sono utilizzati per regolare determinati misurandi. Come regolatori intelligenti 3 azioni in 1, si utilizzano ogni giorno in numerosi sistemi industriali per controllare una variabile in modo estremamente preciso fino al valore di consegna (setpoint). Qui di seguito vi forniremo le informazioni essenziali sulla regolazione PID.
Indice dei contenuti
Che cos'è un controllore PID?
Un controllore compatto può essere impiegato per un'ampia varietà di applicazioni e di solito viene utilizzato come controllore P.I.D. cioè con le azioni regolanti Proporzionale, Integrale e Differenziale (P.I.D.). In questo caso, l'operatore deve procedere e dimensionare le singole azioni in funzione del processo da controllare
- Pb (banda proporzionale),
- Rt (tempo di ripristino) e
- Dt (tempo residuo).
Come funzionano i regolatori PID?
Il principio di funzionamento di un regolatore PID è relativamente semplice da spiegare. Indipendentemente dal tipo di variabile regolata (temperatura o umidità), il regolatore tenta sempre di regolare una specifica variabile di controllo al valore di riferimento ("setpoint") in base al valore effettivo. In questo caso, il componente P amplifica la deviazione di controllo, il componente I aumenta il livello di uscita in caso di deviazione di controllo esistente e il componente D contrasta il movimento del valore effettivo. I componenti non necessari per il controllo possono essere disattivati. A seconda dell'applicazione, vengono quindi definiti come controllori PI, P, PD o I.
In quali applicazioni si utilizzano i controllori PID?
La struttura PID garantisce la migliore risposta di controllo per la maggior parte delle applicazioni. Di conseguenza, i regolatori compatti PID sono molto comuni nel campo del controllo della temperatura. Consentono inoltre un collegamento diretto di sonde di temperatura RTD e termocoppie. Alcune variabili controllate, tra cui la velocità e la portata, richiedono la disattivazione di una o più componenti PID.
Cosa c'è dietro i componenti PID e i rispettivi parametri di controllo?
La componente P reagisce molto velocemente e amplifica la differenza di regolazione; la sua deviazione di regolazione permanente ha un effetto svantaggioso. Il parametro di controllo responsabile è la banda proporzionale Pb. Con una dimensione minore di Pb, il controllore diventa più veloce e la deviazione di controllo più piccola. Tuttavia, il sistema complessivo tende a oscillare in modo crescente.
La componente I elimina la deviazione di controllo. Se il tempo di ripristino Rt è impostato su un valore basso, il regolatore aumenta più rapidamente il livello di uscita e contrasta più velocemente la deviazione di controllo. Tuttavia, se l'impostazione è troppo piccola, si verifica un comportamento oscillatorio.
La componente D contrasta il movimento del valore effettivo. Ciò significa che, per un regolatore di riscaldamento, la componente si riduce quando il valore effettivo aumenta e aumenta quando il valore effettivo diminuisce. Il comportamento descritto ha un effetto di smorzamento. Il parametro responsabile è il tempo di derivata Dt. Maggiore è l'impostazione di Dt, maggiore è l'effetto descritto.
Come possono essere ottimizzati i regolatori PID?
Il comportamento dei sistemi PID dipende sempre dalle condizioni operative. Per questo, prima della parametrizzazione, l'impianto deve essere impostato su uno stato operativo realistico. Ad esempio, un forno deve essere caricato prima con la reale quantità di prodotto e deve essere generato il pilotaggio di un riscaldatore d'acqua istantaneo. La modifica del setpoint, è consentita sia durante l'ottimizzazione che in fasi successive.
Qualora esistano già sistemi di controllo con parametri comparabili, è possibile usare i parametri di controllo ivi utilizzati. Se però questo approccio non portasse all'obiettivo, ovvero ottenere la regolazione ottimale, si potrebbe ricorrere a uno dei seguenti metodi di ottimizzazione.
Il metodo dell'oscillazione secondo Ziegler e Nichols
Questo metodo viene utilizzato per sistemi relativamente veloci. Innanzitutto deve essere configurato il parametro P, partendo da una banda proporzionale (Pb) molto ampia. Nella figura seguente è definito setpoint (W) nel successivo campo di lavoro.
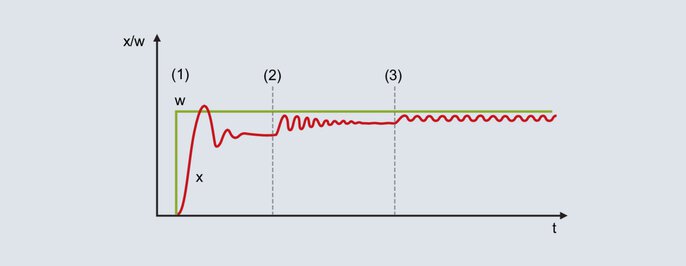
Fig. 52: Curva del valore di riferimento e del valore effettivo quando si utilizza il metodo dell'oscillazione
Con la banda proporzionale relativamente grande, il valore effettivo si sposta verso il valore finale con una scarsa tendenza all'oscillazione [Figura 52 (1)]. A causa della struttura I inesistente, è presente una deviazione di controllo permanente.
Se la Pb viene ridotta (Figura 52 [2]): Il valore effettivo aumenta e si sposta verso il valore finale con una maggiore tendenza all'oscillazione. In alcune circostanze, la banda proporzionale può essere ridotta più volte fino a quando il valore effettivo oscilla in modo permanente. (Figura 52 [3]). La banda proporzionale richiesta affinché si verifichi questo comportamento è chiamata Pbc (Pb critico) e deve essere determinata con la massima chiarezza possibile. (non ridurre Pb a passi troppo grandi).
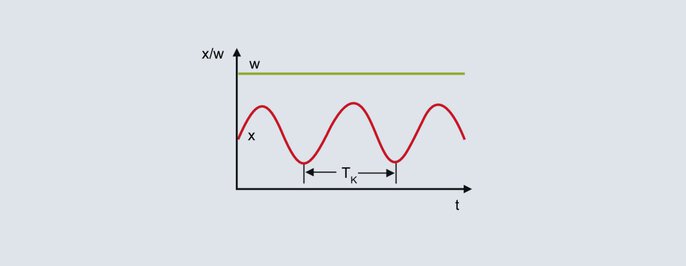
Critical period
Dalla continua oscillazione del valore effettivo nella figura superiore, la durata del periodo critico Tc rappresenta il secondo parametro caratterizzante da determinare per il metodo. La durata del periodo critico Tc (in secondi) viene calcolata, ad esempio, come intervallo di tempo tra i due valori minimi. Per determinare i parametri di controllo Pbc e Tc vanno inseriti nella seguente tabella, in funzione della struttura di controllo prevista (P, PI o PID).
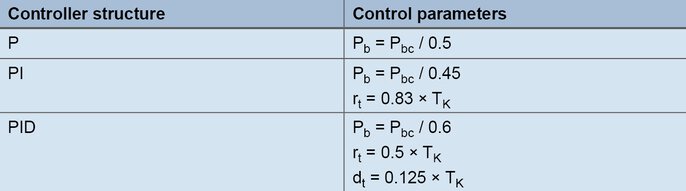
Formule per la configurazione conforme al metodo di oscillazione
Metodo basato sulla risposta delle fasi del processo secondo Chien, Hrones e Reswic
Con questo metodo, i parametri di controllo sono determinati in modo relativamente rapido anche per i sistemi più lenti. Tale metodo è usato per i sistemi di controllo a partire dal secondo ordine e offre la possibilità di distinguere tra formule di comando e in risposta ai disturbi. Per le formule generali, il coefficiente di trasferimento del sistema di controllo, il tempo di ritardo e il tempo di compensazione sono determinati dalla risposta al segnale.
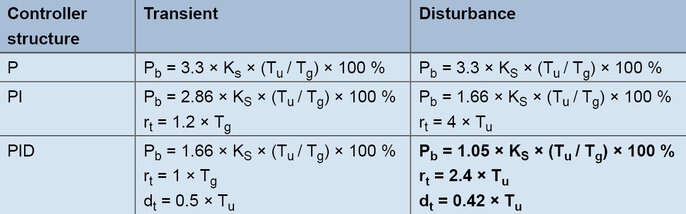
Formule di creazione in base alla risposta del segnale di linea
Esempio:
Un controllore digitale con struttura PID deve essere utilizzato per un forno da laboratorio. L'obiettivo è quello di assicurare un buon funzionamento in presenza di eventuali anomalie; i setpoint tipici sono 200 °C. In modalità manuale, il livello di uscita viene aumentato gradualmente fino a quando il valore effettivo è leggermente inferiore al setpoint successivo (è necessario attendere i processi di compensazione in ogni caso). Ad esempio, si raggiunge una temperatura di 180 °C con un livello di uscita del 60 %. A partire dal 60 %, il livello di uscita viene aumentato gradualmente fino all'80 % e viene registrato il valore effettivo.
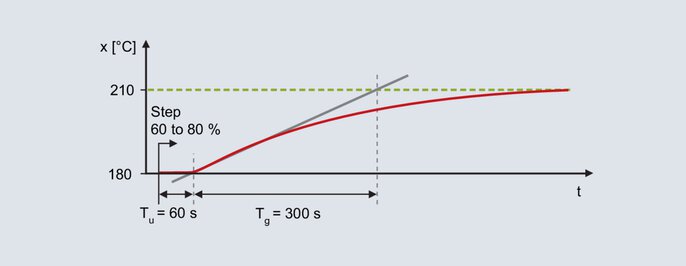
Risposta al segnale del forno da laboratorio
La reazione viene determinata con l'aiuto della tangente di rotazione: Tempo di ritardo Tu = 60 s, tempo di compensazione Tg = 300 s. Il coefficiente di trasmissione del sistema controllato è il risultato della variazione del valore effettivo diviso per il valore di uscita.

Equazione 22
Utilizzando le regole empiriche, si ottengono i seguenti parametri per il comportamento di interferenza:
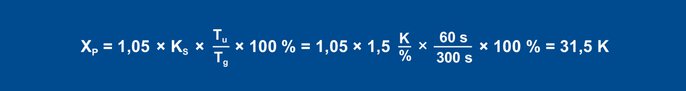
Equazione 23
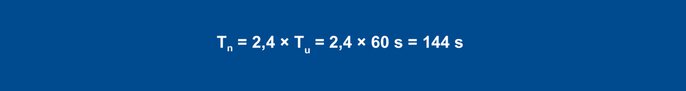
Equazione 24
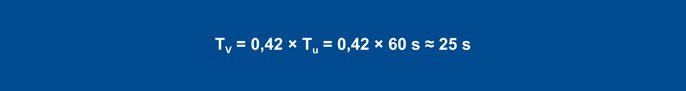
Equazione 25
Il valore di uscita deve essere eseguito nell'intervallo del punto di lavoro successivo. Tuttavia, l'altezza del valore deve essere selezionata in modo tale da poter valutare la curva del valore di processo. Dopo aver specificato il valore di uscita, si attende il valore finale del valore effettivo; un'alternativa per risparmiare tempo è la procedura in base al tasso di incremento.
Procedura conforme al tasso di aumento
Per quanto riguarda la reazione, la procedura è la stessa della risposta al gradino della distanza. Prima del cambio di fase, viene specificato un livello di uscita con il quale il valore effettivo è leggermente inferiore al valore nominale utilizzato successivamente.
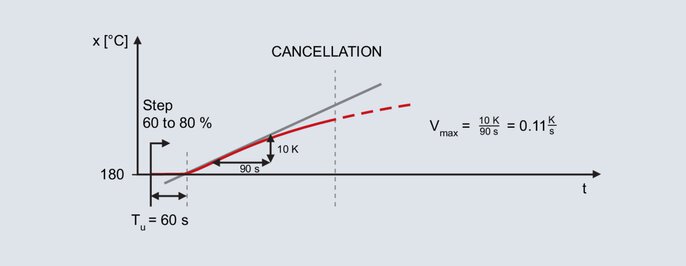
Valore attuale della curva per il metodo in base alla velocità di rotazione
L'impostazione del livello è nuovamente effettuata per il forno da laboratorio già menzionato; anche il successivo punto di funzionamento è di 200 °C. Specificando un grado di funzionamento del 60 % in modalità manuale, si ottiene un valore effettivo di 180 °C. Il livello di uscita viene aumentato per gradi fino all'80 %.
Dopo aver impostato il livello, il valore effettivo aumenta dopo un certo tempo. La registrazione continua finché il valore effettivo non raggiunge la pendenza massima. Anche con questo metodo si traccia la tangente di rotazione e si determina il tempo di ritardo. Il secondo parametro è la velocità massima di salita, che corrisponde alla pendenza della tangente di rotazione. La velocità massima di salita è determinata da un triangolo di pendenza in corrispondenza della tangente di rotazione:
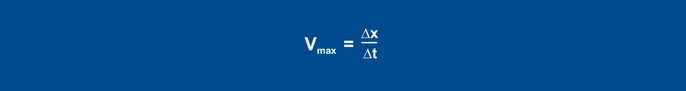
Equazione 26
I valori determinati Vmax (0,11 K/s) e Tu (60 s) sono utilizzati nelle formule seguenti:
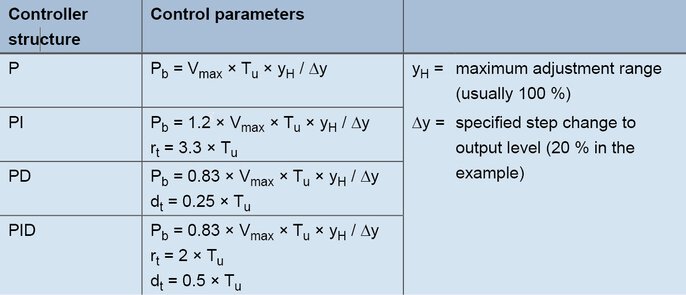
Formule per l'impostazione in base al tasso di crescita
Per un controllore PID, i valori si ottengono con le formule seguenti:

Equazione 27
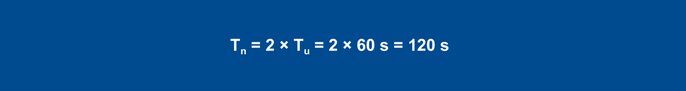
Equazione 28
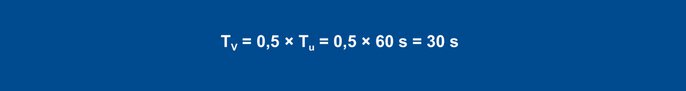
Equazione 29
Metodo empirico per la determinazione dei parametri di controllo
Con questo metodo, le impostazioni favorevoli per i componenti P, D e I vengono determinate una dopo l'altra. Partendo dallo stato iniziale (livello di uscita 0 %), viene sempre specificato il setpoint tipico; pertanto, il metodo può essere utilizzato solo per sistemi controllati in modo relativamente rapido (ad esempio, sistemi controllati in modo rapido della temperatura e variabili controllate come la velocità o la portata).
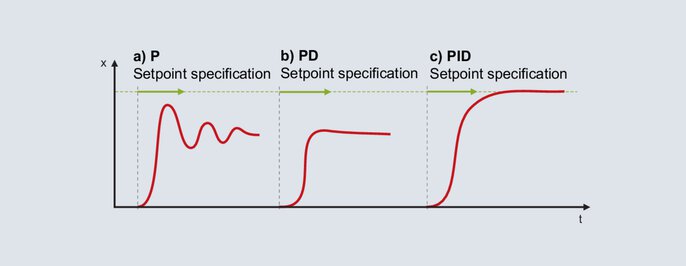
Configurazione del regolatore PID in base al metodo empirico
La struttura P è attivata per il regolatore digitale. La banda proporzionale è impostata relativamente grande (il dimensionamento dipende dal sistema controllato) e il setpoint è specificato nell'intervallo di funzionamento successivo. Il valore effettivo si avvicinerà lentamente al valore finale e ne risulterà una deviazione di regolazione relativamente grande. Successivamente, il setpoint viene specificato con una banda proporzionale XP sempre più ridotta. L'obiettivo è un Xp al quale il valore effettivo raggiunge il valore finale stabile dopo due o tre oscillazioni complete (Figura 56a). Per un avvio smorzato, la struttura passa da P a PD. Partendo da una piccola impostazione del tempo di derivazione, il setpoint viene specificato con un Tv sempre maggiore. Se il valore del processo raggiunge il valore finale con la minima oscillazione possibile, è presente un Tv favorevole (Figura 56b).
Nota: non appena il regolatore imposta il livello di uscita a 0 % anche una sola volta durante l'avvio, il Tv è impostato troppo alto.
Per alcune linee non è possibile attivare tutti i componenti. Se la struttura P comporta un comportamento instabile già per grandi impostazioni di XP, non è possibile utilizzare né la struttura P né la struttura D. Si utilizza il regolatore I. Viene utilizzato il controllore I.
Se l'ottimizzazione del controllore P ha avuto successo, ma l'introduzione della componente D rende l'anello di controllo instabile, si utilizza la struttura PI.
Come si può ri-ottimizzare manualmente un controllore PID?
L'applicazione dei metodi di ottimizzazione presentati darà molto probabilmente come risultato un comportamento di controllo stabile, ma non ottimale. La post-taratura manuale migliorerà ulteriormente il risultato del controllo. Se il funzionamento di un controllore PID può essere assegnato a una delle curve da 62b a 62e, le istruzioni per un'ulteriore ottimizzazione sono riportate di seguito.
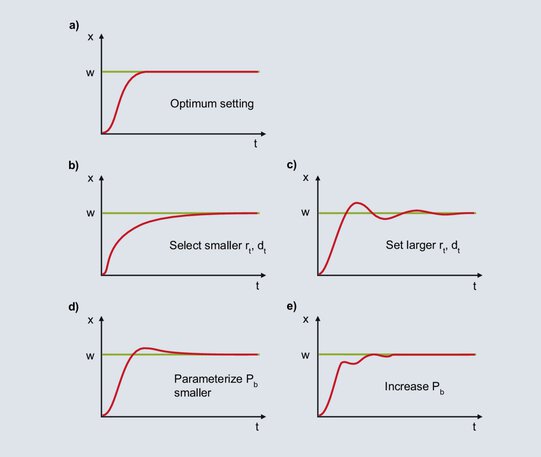
Fig. 62: Note a seguito della taratura di un regolatore PID
a)
Il diagramma mostra un funzionamento ottimale per un controllore PID.
b)
Dopo aver specificato il setpoint, il valore di processo aumenta bruscamente fino a raggiungere la banda proporzionale. Quando il valore di processo raggiunge la banda proporzionale, la componente P si riduce e la componente I assicura il raggiungimento del valore nominale. A causa dell'impostazione relativamente ampia di Tn, l'aumento della componente I è lento e la deviazione di controllo viene eliminata lentamente. Per un'integrazione più rapida, Tn deve essere impostato più basso; anche Tv viene ridotto in base al rapporto Tv/Tn = 1/4.
c)
Quando il valore del processo entra nella banda proporzionale, il componente I aumenta il rapporto di uscita. L'aumento continua finché il valore di processo non raggiunge il setpoint. Nel caso illustrato, la componente I aumenta troppo l'uscita fino a quando la deviazione di controllo viene eliminata e il valore di processo supera il setpoint. In presenza di una deviazione negativa del sistema, il livello di uscita si riduce troppo rapidamente, il valore effettivo scende al di sotto del setpoint, ecc. L'oscillazione simmetrica del valore effettivo intorno al setpoint indica che Tn è impostato troppo basso. Tn deve essere aumentato e anche Tv deve essere aumentato secondo il rapporto Tv / Tn = 1/4.
d)
La componente I si forma dal momento in cui il valore di processo entra nella banda proporzionale fino all'eliminazione della deviazione di regolazione. A causa dell'ampia impostazione di Xp, la componente I inizia a formare il rapporto di uscita già in presenza di un'ampia deviazione di controllo. A causa dell'ampia deviazione di controllo iniziale, il componente I forma il suo rapporto di uscita in modo relativamente rapido. Quando la deviazione di regolazione viene eliminata, la componente I è troppo grande e il valore effettivo supera il valore nominale. Con un'impostazione più bassa di Xp, la componente I inizia a formare il suo livello di uscita in modo proporzionalmente più lento solo con deviazioni di controllo minori. Il superamento una tantum mostrato diventa meno probabile.
e)
Se XP è impostato troppo basso, il livello di uscita del componente P si riduce poco prima del raggiungimento del setpoint. Quando il valore di processo entra nella banda proporzionale, la componente P si riduce molto e il valore di processo diminuisce. A causa della maggiore deviazione di controllo, il rapporto di uscita aumenta e il valore effettivo sale. Nella banda proporzionale, piccole variazioni del valore effettivo portano a grandi variazioni del rapporto di uscita, con conseguente elevata tendenza all'oscillazione. L'aumento della banda proporzionale consente di stabilizzare la situazione.
- ${title}${badge}


